前言

以下範例利用 QDA 對具有 2 個變數的資料分為 2 個群組，展示 QDA 如何利用資料為多變量常態分配的假設計算出決策邊界，並說明 QDA 的決策邊界限制式之最高次為二次方，此為 QDA 名稱中 Q（Quadratic）的由來。

QDA 在兩群組下的分群邊界

假設資料存在群組 k 與群組 l，共 2 個群組，分別為隨機變數向量 [X1, X2]'，且其服從多變量常態分配，群組分別具均數向量與正定的共變義數矩陣

取判定函數相等的樣本集合為決策邊界，並設向量 x = [x1, x2]' 。則此時，樣本之子集合

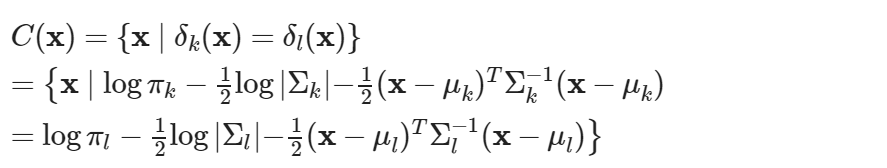
為群組 k、l 之間的決策邊界。

QDA 名稱之由來

QDA 的決策邊界限制式的最高次為二次方，此為 QDA 名稱中 Q（Quadratic）的由來。若要觀察，將上式之決策邊界展開，可得到決策邊界

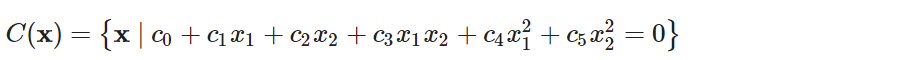
集合的限制條件為多項方程式之型式，其中，ci, i=0, 1, ..., 5 為不含 x1, x2 的常數，其分別為

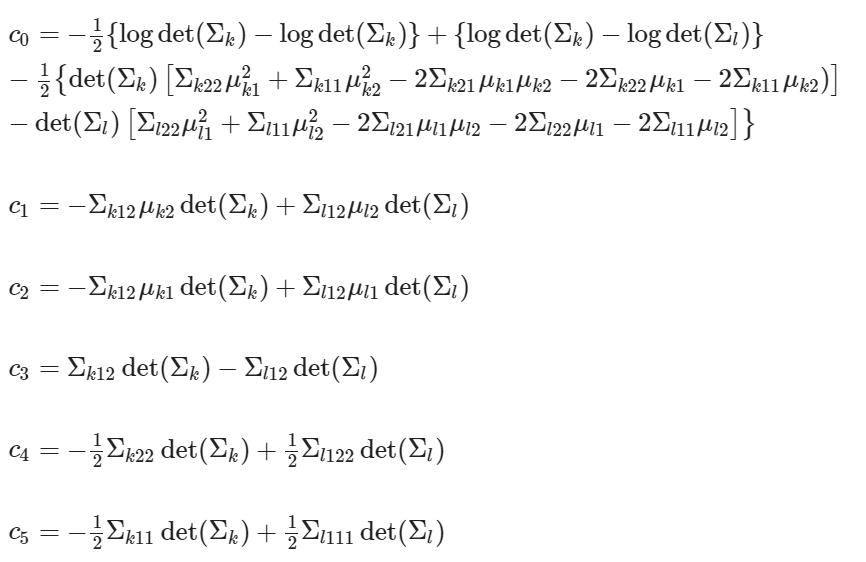
上式中，集合的限制條件之多項方程式最高項為二次方，係平面上的二次曲線。

如果近一步將所欲分群的資料之群組數量從 2 群擴大為 n 群，可看出決策邊界的條件之最高項依舊為二次，不因群數增加而變化。因此，QDA 的決策邊界之樣本子空間的最高次為二次方，此為 QDA 名稱中 Q（Quadratic）的由來。故 QDA 的含意為：假設各群資料為不全相同之共變異數矩陣的多變量常態分配，分群方法為二次的（Quadratic）之判定分析（Discriminant Analysis）。

把原來矩陣與向量組成的判定函數展開成多項方程式的過程花了筆者約 40 分鐘的時間，包含展開數式並檢查是否有乘錯，真的很久。如果有發生計算錯誤，請見諒，並煩請不吝於下方留言點出錯誤的地方，感謝您！

參考資料

統計觀念

• Johns Hopkins University - Advanced Methods in Biostatistics 2 (140.752) - Notes - The different of multivariate normal distribution with a semi-positive definite and one with positive definite variance-covariance matric.

• Reject Region : Casella, G., & Berger, R. L. (2002). Statistical inference. 2nd ed (pp. 374). Australia ; Pacific Grove, CA, Thomson Learning.

QDA 數學推導過程
（Google 關鍵字： QDA MULTIVARIATE NORMAL）

• Stanford University - STATS 202: Quadratic discriminant analysis (QDA)
• Penn State University - STAT 505 Applied Multivariate Statistical Analysis: Lesson 10: Discriminant Analysis

線性代數

• Trace : Wiki Trace (linear algebra)-Properties of Trace
• 內積 : Wiki 內積-性質
• 二次式之 Trace 特性 : The Multivariate Normal Distribution 簡報第20頁
• 二次式之 Trace 與偏微分 : CHAPTER 13. THE MULTIVARIATE GAUSSIAN, page 8.

其他相關重要觀念

• 下圖擷取自參考資料中的 Johns Hopkins University 的 Ingo Ruczinski 教授，對 Advanced Methods in Biostatistics 2 (140.752) 筆記中第 14 頁。其中重點在於：儘管多變量常態分配只需共變義數矩陣為非負定，但是若要寫出他的 PDF，還需要有更強的條件，即共變義數矩陣為正定。若只為非負定，則其 PDF 不存在。

• 下圖擷取自參考資料中 Statistical inference. 2nd ed (pp. 374)，說明假設檢定過程或假設檢定的定義，還有 Reject Region 或稱 Critical Region 為樣本的子集合。